Console Mandelbrot in FORTH

I really like to play around with FORTH. It’s a “weird” programming language compared to all the other ones I’ve learned over time. There are already many articles out there about why you should give it a try, the best probably being this one at Hackaday.

One little program that is often demonstrate on old computers is a BASIC program to compute the Mandelbrot Set in the console. I thought I’d try my hand in “converting” the program to FORTH.

Here’s my version, taken from a gist I wrote earlier this year.

\ from proposal http://www.forth200x.org/fvalue.html
variable %var
: to 1 %var ! ;
: fvalue create f, does> %var @ if f! else f@ then 0 %var ! ;

0e0 fvalue i3
0e0 fvalue r3

59 value x1
21 value y1
-1e0 fvalue i1 
1e0 fvalue i2
-2e0 fvalue r1
1e0 fvalue r2
r2 r1 f- x1 s>f f/ fvalue s1 \ L30
i2 i1 f- y1 s>f f/ fvalue s2 \ L31

0e0 fvalue a
0e0 fvalue b
: single_iter { F: z1 F: z2 } ( F: z1 F: z2 -- F: z1' F: z2' F: mag )
  z1 fdup f* to a \ L90
  z2 fdup f* to b \ L91
  a b f- r3  f+ \ z1 \ L111
  2e0 z1 z2 f* f* i3 f+ \ z2 L110
  a b f+ \ mag \ line 100
;

: print_char ( F: x F: y -- )
  30 \ push the max in case we don't exit early
  30 0 do                          \ L80
    single_iter
    4e0 f> if drop i leave then
  loop                             \ L120
  fdrop fdrop \ clean z1 and z2
  62 swap - emit                   \ L130
;

: calc_i3 { y }
  i1 s2 y s>f f* f+ to i3 \ L50
;

: calc_r3 { x }
  r1 s1 x s>f f* f+ to r3 \ L70
;

: mandel
cr \ always start on a fresh clean line
y1 0 do                         \ L40
  i calc_i3
  x1 0 do                       \ L60
    i calc_r3
    r3 i3 print_char
  loop                            \ L140
  cr                              \ L150
loop                              \ L160
;

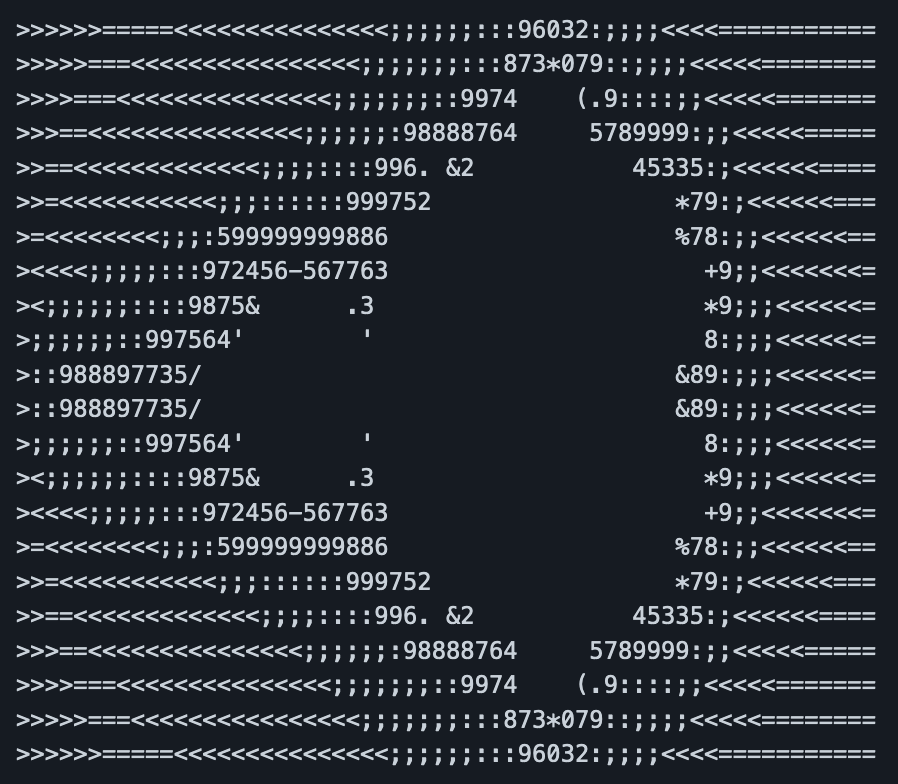
mandel

That prints out something like the screenshot at the top of this post.

The “L##” comments roughly refer to the lines in the BASIC version, if you’d like to compare the two. I tried to keep the memory usage and general complexity as equal as possible – that’s why there are so many value and fvalue variables. I’ve seen some examples that use the stack more but are harder to read and have to recompute a lot of things that the BASIC version doesn’t.

Here’s the original BASIC version:

10 x1=59
11 y1=21
20 i1=-1.0
21 i2=1.0
22 r1=-2.0
23 r2=1.0
30 s1=(r2-r1)/x1
31 s2=(i2-i1)/y1
40 for y=0  to y1
50 i3=i1+s2*y
60 for x=0 to x1
70 r3=r1+s1*x
71 z1=r3
72 z2=i3
80 for n=0 to 29
90 a=z1*z1
91 b=z2*z2
100 if a+b>4.0 goto 130
110 z2=2*z1*z2+i3
111 z1=a-b+r3
120 next n
130 print chr$(62-n);
140 next x
150 print
160 next y
170 end

I’m consistently intrigued by FORTH, so I’ll probably be sharing more programs and thoughts. I wrote a short explanation of the “polyfill” in the first four lines of the FORTH version is actually a great dive into the language’s extensibility.